19. Сущность и реализация метода статистических испытаний

Метод статистического моделирования заключается в воспроизведении исследуемого процесса при помощи вероятностной математической модели и вычислении характеристик этого процесса. Основан метод на многократном проведении испытаний построенной модели с последующей статистической обработкой полученных данных с целью определения характеристик рассматриваемого процесса в виде статистических оценок его парамнам известен.

Рассмотрим уравнение:

Если функция f существенно нелинейна, то для решения данной задачи нет универсальных методов решения, и достаточно полно отработанные регулярные методы поиска оптимальных решений можно применить только поставив во главу угла видимость использования математики, упрощения приведут к серьезной потери точности. Математическая модель станет неадекватной исследуемой системе, и моделирование будет только формой заблуждения.

В методе статистических испытаний для получения достаточно надежных результатов необходимо обеспечивать большое число реализаций N, кроме того, с изменением хотя бы одного исходного параметра задачи необходимо производить серию из N испытаний заново. При сложных моделях неоправданно большая величина N может стать фактором, задерживающим получение результата. Поэтому важно правильно оценить необходимое число результатов.

При построении статистических моделей информационных систем используется общий и прикладной математический аппарат. В качестве примера можно привести аппарат систем массового обслуживания. Система массового обслуживания (СМО) - система, предназначенная для выполнения потока однотипных требований случайного характера. Статистическое моделирование СМО заключается в многократном воспроизведении исследуемого процесса (технического, социального и т.д.) при помощи вероятностной математической модели и соответствующей обработке получаемой при этом статистики. Существуют пакеты программ статистического моделирования СМО, однако они требуют определенных усилий для их освоения и не всегда доступны. Поэтому в рамках дисциплины предлагается достаточно простой подход, позволяющий с наименьшими затратами моделировать простые СМО. При этом предполагается, что пользователь ознакомлен с теорией массового обслуживания и имеет навыки работы на компьютере. Следует помнить, что массовое обслуживание - важный, но далеко не единственный предмет статистического моделирования. На основе этого метода решаются, например, задачи физики (ядерной, твердого тела, термодинамики), задачи оптимизации маршрутов, моделирования игр и т.п.

Обобщенные алгоритмы статистического моделирования Существуют две схемы статистического моделирования: - моделирование по принципу особых состояний; - моделирование по принципу дельта t.

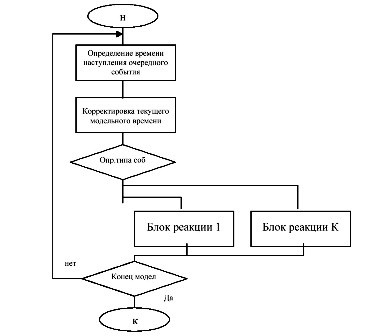
Порядок моделирования по принципу особых состояний заключается в выполнении следующих действий: 1) случайным образом определяется событие с минимальным временем - более раннее событие; 2) модельному времени присваивается значение времени наступления наиболее раннего события; 3) определяется тип наступившего события; 4) в зависимости от типа наступившего события осуществляется выполнение тех или иных блоков математической модели; 5) перечисленные действия повторяются до истечения времени моделирования.

В процессе моделирования производится измерение и статистическая обработка значений выходных характеристик. Эта схема моделирования хорошо подходит для систем массового обслуживания в традиционном их описании. Обобщенный алгоритм моделирования по принципу особых состояний представлен схемой на рис.

Моделирование по принципу дельта t осуществляется следующим образом: 1) устанавливаются начальные состояния, в т. ч. t = 0; 2) модельному времени дается приращение t =t+дельта t; 3) на основе вектора текущих состояний элементов модели и нового значения времени рассчитываются новые значения этих состояний; за дельта t может наступить одно событие, несколько событий или же может вообще не происходить событий; пересчет состояния всех элементов системы – более трудоемкая процедура, нежели любой из блоков реакции модели, построенной по принципу особых состояний; 4) если не превышено граничное время моделирования, предыдущие пункты повторяются.

В процессе моделирования производится измерение и статистическая обработка значений выходных характеристик. Эта схема моделирования применима для более широкого круга систем, нежели моделирование по принципу особых событий, однако есть проблемы с определением дельта t. Если задать его слишком большим - теряется точность, слишком малым - возрастает время моделирования.

На основе базовых схем моделирования можно строить комбинированные и диалоговые схемы, в которых моделирование идет под контролем оператора с возможностью внесения изменений как в исходные данные, так и в математическую модель процесса.

Структура алгоритма модели, построенной по принципу дельта t, проще структуры, построенной по принципу особых состояний. Программная реализация моделей, построенных по одной и той же реальной системе в одной и той же системе программирования, но по разным принципам статистического моделирования, имеет практически одинаковую трудоемкость.